WSDM 25唯一最佳论文：从谱视角揭开推荐系统流行度偏差放大之谜

近日，第 18 届国际互联网搜索与数据挖掘大会（The 18th International Conference on Web Search and Data Mining, WSDM 2025）在德国汉诺威召开。本届会议共收录了 106 篇论文，荣获大会唯一的一篇最佳论文奖（Best Paper Award）来自中国。

 

 

论文地址：https://arxiv.org/abs/2404.12008

 

这篇最佳论文题目为：How Do Recommendation Models Amplify Popularity Bias? An Analysis from the Spectral Perspective/ 推荐模型如何放大流行度偏差？——基于谱视角的分析，由浙江大学计算机科学与技术学院 ZLST 实验室团队与中国科技大学、蚂蚁集团联合撰写。

 

 

这篇论文揭示了推荐系统流行度偏差放大的原因，研究团队发现：

 

• 流行度存储效应：推荐模型的评分矩阵的最大奇异向量（第一主成分）与物品的流行度向量高度相似，流行度信息几乎完全由主特征向量所捕获。
• 流行度放大效应：维度缩减现象加剧了流行度偏差的「放大效应」，主要源于推荐模型中用户和物品 Embedding 的低秩设定以及优化过程中的维度缩减。

 

为了解决这个问题，研究团队提出了一种基于正则项的方法——ReSN，通过在推荐模型的损失函数中引入谱范数正则项，约束评分矩阵的谱的权重（最大奇异值），从而缓解流行度偏差。

 

研究动机

 

推荐系统是基于用户的历史行为数据进行个性化推荐的核心技术。但你知道吗？推荐系统往往「偏爱」热门内容。

 

比如，在 Douban 数据集中，前 0.6% 热门物品占模型推荐物品的超过 63%，前 20% 的热门物品占了推荐列表的 99.7%。这导致冷门物品几乎无缘被推荐，用户陷入「信息茧房」，无法发现更多新鲜、有趣的内容。

 

 

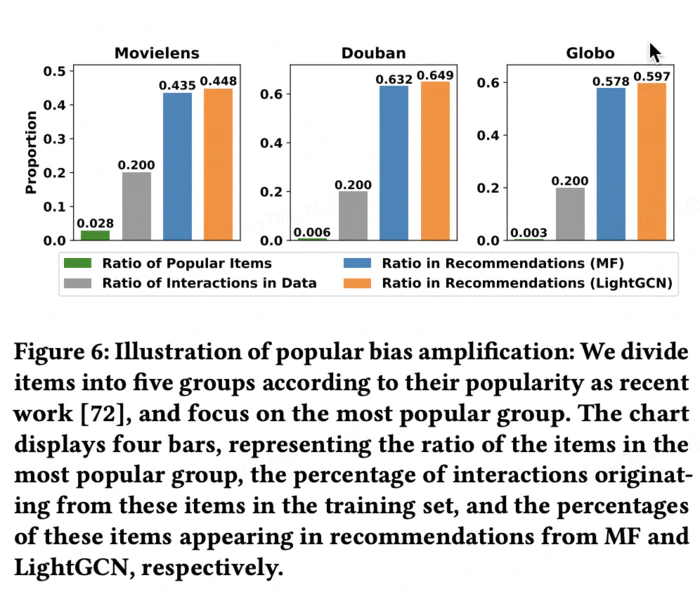
这要从数据的长尾分布开始说起，用户行为数据和物品的流行度通常呈现长尾分布，而推荐模型在这样长尾分布的数据上训练学习，不仅会继承这种倾斜的分布，甚至会放大，导致热门物品被过度推荐。

 

推荐系统为什么会放大流行度偏差呢？

 

核心发现

 

1. 流行度记忆效应：推荐模型的评分矩阵的最大奇异向量（第一主成分）与物品的流行度向量高度相似，最大奇异向量几乎完全捕获了物品的流行度特性。

 

实验发现，多个推荐模型的评分矩阵的最大奇异向量（第一主成分）与物品的流行度向量的余弦相似度超过 98%!

 

 

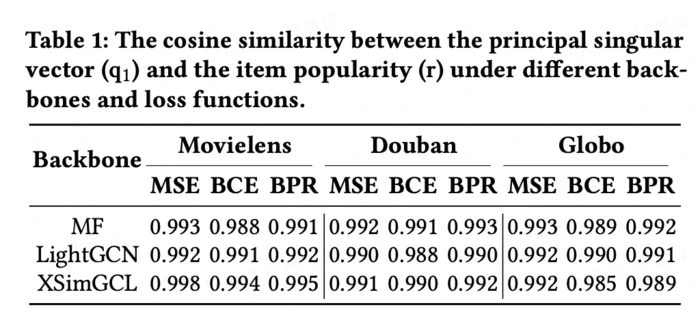
上述现象并不是偶然的，而有严格的理论支撑！对于有 n 个用户、m 个物品的推荐系统，设推荐模型给出的评分矩阵为，我们将评分矩阵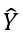SVD 分解为，其中最大奇异值对应的右奇异向量 q_1 捕获到了物品流行度 r∈R^m 的信息。特别地，当物品的流行度满足以 α 为参数的幂律分布时（即第 g 最流行的物品的流行度），我们证明了：

 

 

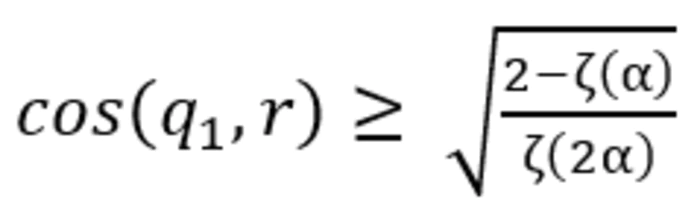
其中，为 Riemann zeta 函数，满足 α→∞ 时 ζ(α)→1。此时，当流行度偏差非常严重，也即 α 很大时，上面的不等式右侧可以近似为 1。这验证了我们的实验发现，即评分矩阵最大奇异值对应的右奇异向量 q_1 记忆了物品流行度 r 的信息。对于一般情况以及证明感兴趣的同学们可以看原文！

 

2. 流行度放大效应：维度缩减现象加剧了流行度偏差的「放大效应」。

 

上面关于流行度记忆效应的分析说明物品流行度对推荐系统的预测结果有着举足轻重的影响。更进一步地，经验发现，即使前 0.6% 热门物品的流行度总和只占总流行度 20%，模型的推荐结果最终有多达 63% 属于这些热门物品！这说明推荐模型会放大流行度偏差！问题在于，这一现象的背后原理是什么呢？

 

我们的研究表明，低秩近似带来的维度缩减现象是罪魁祸首！具体来说：

 

1. 推荐模型中用户和物品 Embedding 通常设置为低维（低秩），这种低秩设定会放大评分矩阵中最大奇异值的相对重要性，进而加剧流行度偏差；
2. 优化过程中，最大奇异值增长优先且迅速，其他奇异值增长缓慢，导致模型更多依赖最大奇异特征（即流行度特征），从而进一步增强热门物品在推荐列表中的比例。

 

实验发现当 Embedding 维度减少时，主奇异值的相对重要性显著上升，推荐结果中热门物品的比例也随之增加。

 

实验还发现训练过程中的奇异值分布动态：早期主奇异值快速增长，这与热门物品的优先推荐趋势一致。随着训练继续，尾部奇异值增长滞后，流行度偏差仍保持较高水平。

 

 

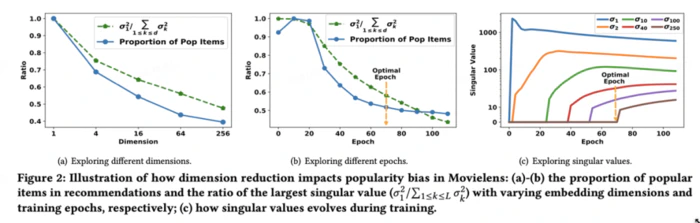
我们也从理论角度建立了奇异值分布与推荐中热门物品比例之间的关系，感兴趣的同学们可以看原文！

 

新方法：基于约束谱范数的纠偏方法 ReSN

本论文的解决方法——ReSN (Regulating with Spectral Norm)，核心是通过正则化谱范数（主奇异值）来抑制流行度偏差，优化目标函数如下所示：

 

 

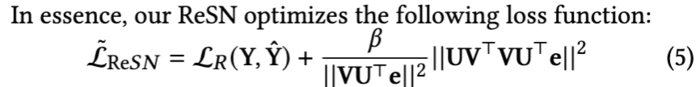
其中，代表原始推荐损失，表示矩阵的谱范数（用于衡量主奇异值），则是用于控制正则化项权重的参数。

 

然而，在实际计算过程中，面临着诸多严峻挑战。一方面，评分矩阵 Y ̂∈R^(n×m)，通常具有庞大的规模，这使得直接计算其谱范数所需的计算资源和时间成本极高，几乎难以实现。另一方面，传统计算谱范数梯度的方法大多是迭代式的，这无疑进一步加重了计算开销，导致模型训练效率极为低下。

 

改进策略

 

简化谱范数计算：利用主奇异向量与物品流行度向量之间的对齐关系，将复杂的矩阵谱范数计算转化为相对简单的向量 L2 范数计算。具体来说，当主奇异向量 q_1 与物品流行度 r 几乎一致时，评分矩阵的谱范数可以近似为，而流行度向量可以表示为，其中 e 为全 1 向量。

 

挖掘矩阵 Y 低秩特性：通过约束矩阵 UV 的（其中 U 和 V 分别表示用户和物品的嵌入矩阵）的谱范数来避免直接处理庞大的矩阵，从而提高计算效率。

 

具体来说，模型的评分矩阵通常由计算得到，其中μ 为激活函数。为了方便计算，我们直接在激活函数前约束谱范数，其中为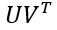的主成分奇异向量。类似地采用之前的谱范数计算的简化方法，我们可以将用近似代替。因此，优化后的损失函数为：

 

 

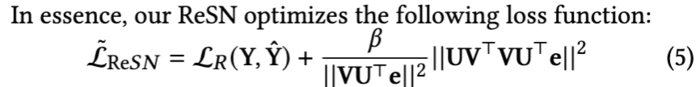
ReSN 方法不依赖后处理，直接在训练中去偏，从源头解决问题。

 

高效轻量，避免了庞大矩阵的直接计算，训练效率高！

 

实验亮点

 

在七个真实数据集上的实验验证中，ReSN 全面优于其他方法。

 

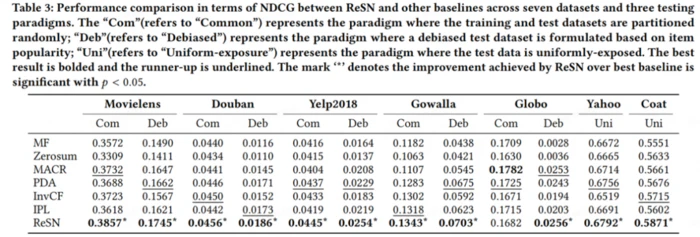
主性能实验：ReSN 在推荐整体准确性和纠偏性两方面都表现突出，在 IID 场景（Com）和 OOD 场景（Deb）中都稳定超越基线方法。

 

 

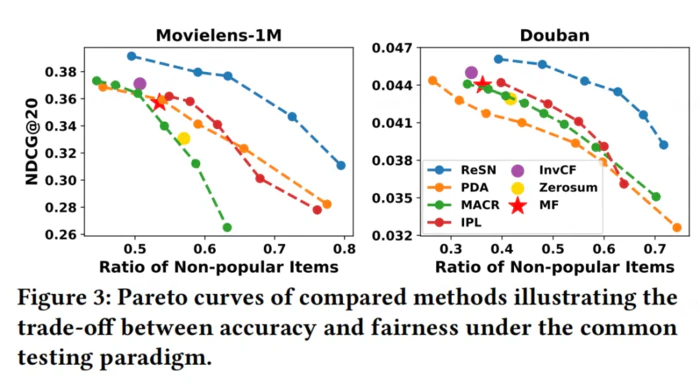
准确性-公平性权衡：我们进一步探究准确性-公平性之间的权衡，实验结果表明，ReSN 的帕累托曲线均在基线方法的右上角，即在相同推荐公平性下实现了更好的性能，同时在相同性能下有更好的推荐公平性。

 

 

总结

研究团队的研究不仅揭示了推荐系统流行度偏差放大的深层原因，还提出了高效的纠偏策略，为推荐系统的优化提供了重要思路和有效解决方案。

©（文：机器之心）

版权声明

本站仅分享教程，不提供任何指导，不会操作请参考教程说明自行研究，小白请勿下单！
客服不回复任何教程内容相关咨询。
虚拟商品购买须知： 虚拟商品具有可复制性，一经打赏赞助，不支持退款。请谅解，谢谢合作！
本站内容转载于网络，版权归原作者所有，仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任，如果侵犯了您的权益，请联系站长 QQ：2428-6070 进行删除。